Grafieken visualiseren cijfers en lijken daardoor betrouwbaar, maar ze kunnen misleidend zijn. Zoals in het voorbeeld hieronder. (Lees ook ons artikel over de drie standaardtrucs van misleidende grafieken en hoe je jezelf daartegen kunt wapenen).
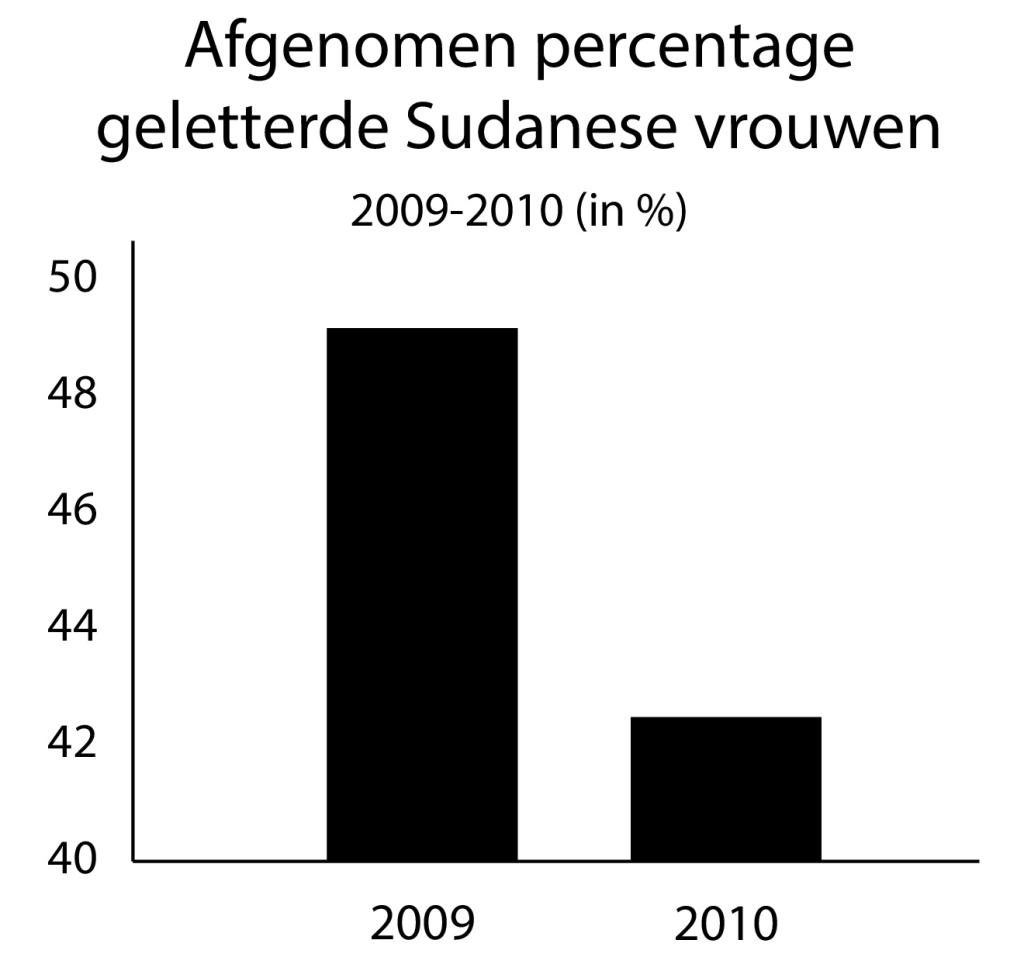
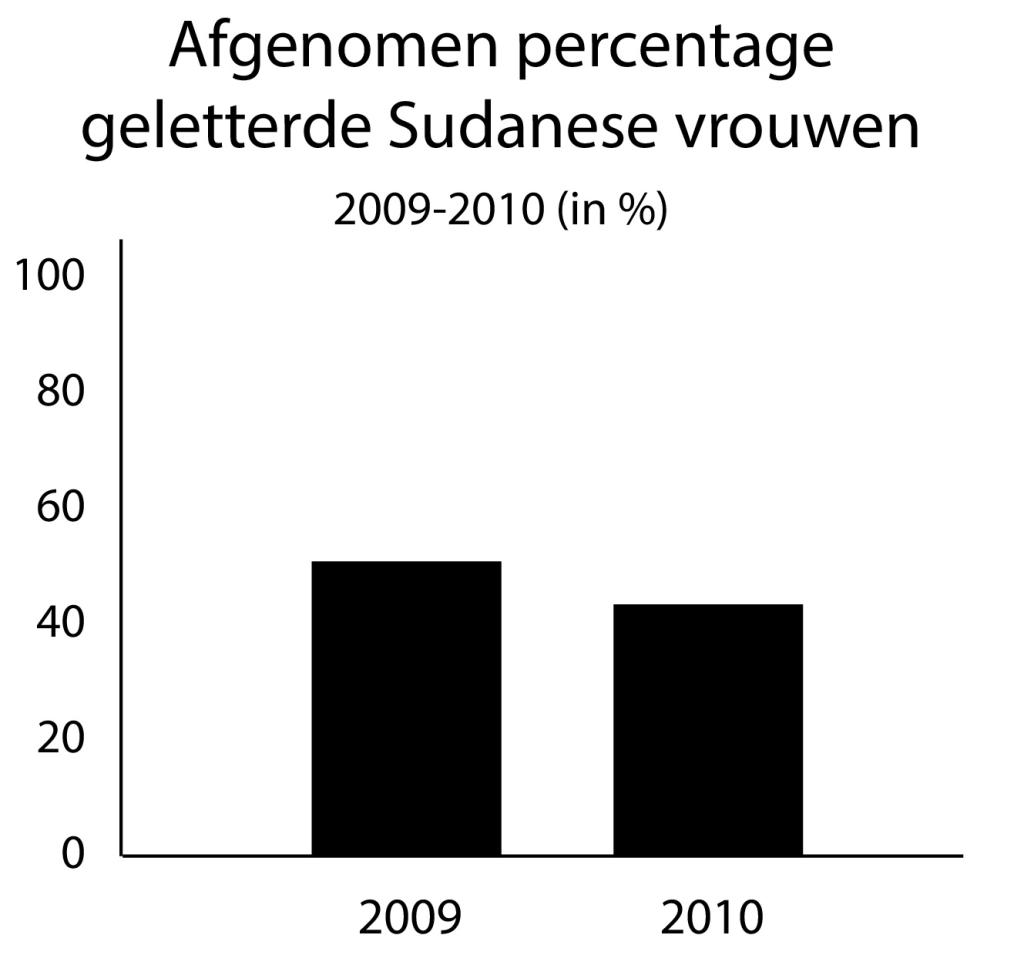
Een voorbeeld: in de twee grafieken hieronder zijn de data dezelfde, maar doordat in de eerste grafiek de verticale as niet op 0 begint, lijkt het verschil tussen de twee jaren daarin groter dan in de correcte grafiek eronder.
Regels voor grafieken
Voor het ontwerp van elk type grafiek bestaan geschreven en ongeschreven regels. Die ontwerpconventies zorgen ervoor dat lezers de data gemakkelijk en correct kunnen aflezen. Als grafiekmakers ervan afwijken, worden grafieken in het gunstigste geval slecht leesbaar en in het slechtste misleidend.
Wij hebben getest hoe je zulke misleidende grafieken effectief kunt corrigeren. Het experiment draaide om staafdiagrammen met een afgesneden verticale as, zoals in het voorbeeld hierboven, een veelvoorkomende vorm van misleiding. In staafdiagrammen moeten de lengtes van de staven weergeven hoe hoeveelheden zich tot elkaar verhouden. Door de verticale as af te snijden, vergroot je de verschillen tussen de staven uit.
Uit het onderzoek blijkt dat mensen het meest gebaat zijn bij een correctie die laat zien hoe de grafiek eruit ziet als de y-as bij 0 begint.
Eerst kijken, dan zien
Voor het onderzoek ontwikkelden we vier methoden om grafieken met misleidend afgekapte verticale assen te corrigeren. Deze methodes zijn gebaseerd op de twee fases die lezers doorlopen wanneer zij een grafiek lezen: eerst een fase van kijken, dan een fase van zien.
Fase 1: Kijken
De eerste fase verloopt intuïtief: van grote vormen nemen we aan dat ze een grote hoeveelheid representeren, een opgaande lijn betekent een toename en dingen die dicht bij elkaar staan horen ook bij elkaar.
Deze eerste fase verloopt voor iedereen vrijwel gelijk, ongeacht opleiding, leeftijd of culturele achtergrond. Wat mensen in deze fase waarnemen, is bepalend voor hun beoordeling van de achterliggende data. Dit is dus ook de fase waarin een uitvergroot verschil misleidend kan werken.
Fase 2: Zien
De tweede fase verloopt rationeler. Dan activeren lezers aangeleerde kennis over grafieken. We lezen labels van de assen, de legenda en we proberen datapunten te interpreteren. Opleiding en ervaring met grafieken lezen (‘grafiekgeletterdheid’) hebben in deze fase een grote invloed.
Nieuwe informatie die iemand in deze tweede fase vindt, kan helpen om het oordeel uit de eerste fase bij te stellen. Toch is de beschermende werking van deze fase tegen misleiding heel beperkt, bleek ook uit dit onderzoek.
Misleiding corrigeren: vier methodes
Om lezers, ongeacht hun grafiekgeletterdheid, te helpen om misleiding te doorzien en grafieken beter te beoordelen, zijn voor het onderzoek verschillende correctiemethodes ontwikkeld die gericht ingrijpen op deze fases.
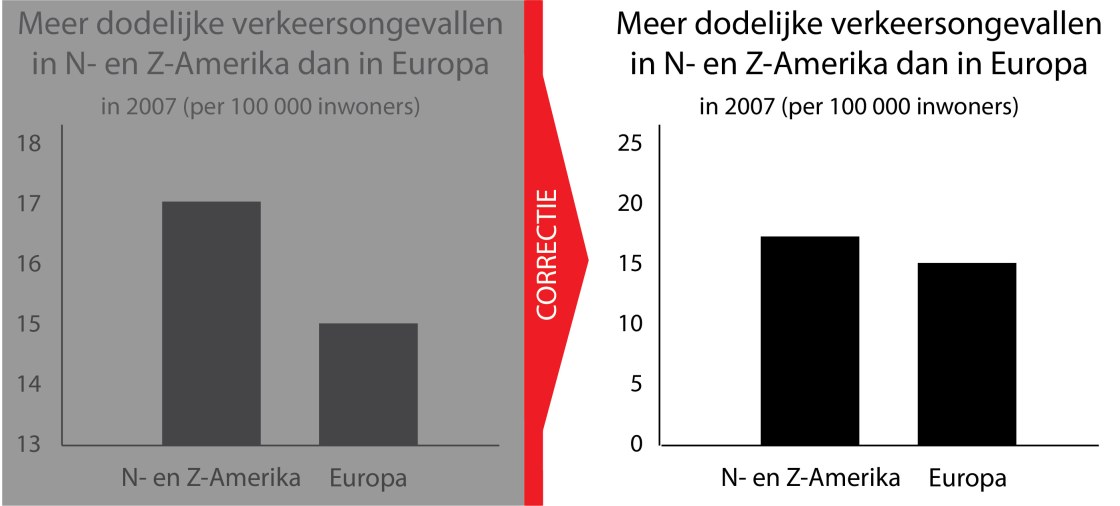
Correctiemethode A grijpt in op de eerste, intuïtieve fase door een correct alternatief van de misleidende grafiek te laten zien. Doel van deze methode is om het misleidende beeld als het ware te overschrijven.
Correctiemethodes B, C en D grijpen in op de tweede, rationele fase door grafiekvaardigheden te activeren. Dat gebeurt door de lezer een visuele (B) of tekstuele (C) aanwijzing te geven die de aandacht vestigt op de afgesneden verticale as, of door een tekstuele aanwijzing die mensen waarschuwt voor mogelijke verdraaiing van de feiten (D).
Correctiemethode A laat de gecorrigeerde grafiek zien met y-as die bij 0 begint:
Correctiemethodes B, C en D grijpen in op de tweede, rationele fase door grafiekvaardigheden te activeren. Dat gebeurt door de lezer een visuele (B) of tekstuele (C) aanwijzing te geven die de aandacht vestigt op de afgesneden verticale as, of door een tekstuele aanwijzing die mensen waarschuwt voor mogelijke verdraaiing van de feiten (D).
Correctiemethode B waarschuwt lezers met een pijl voor de afgesneden y-as:
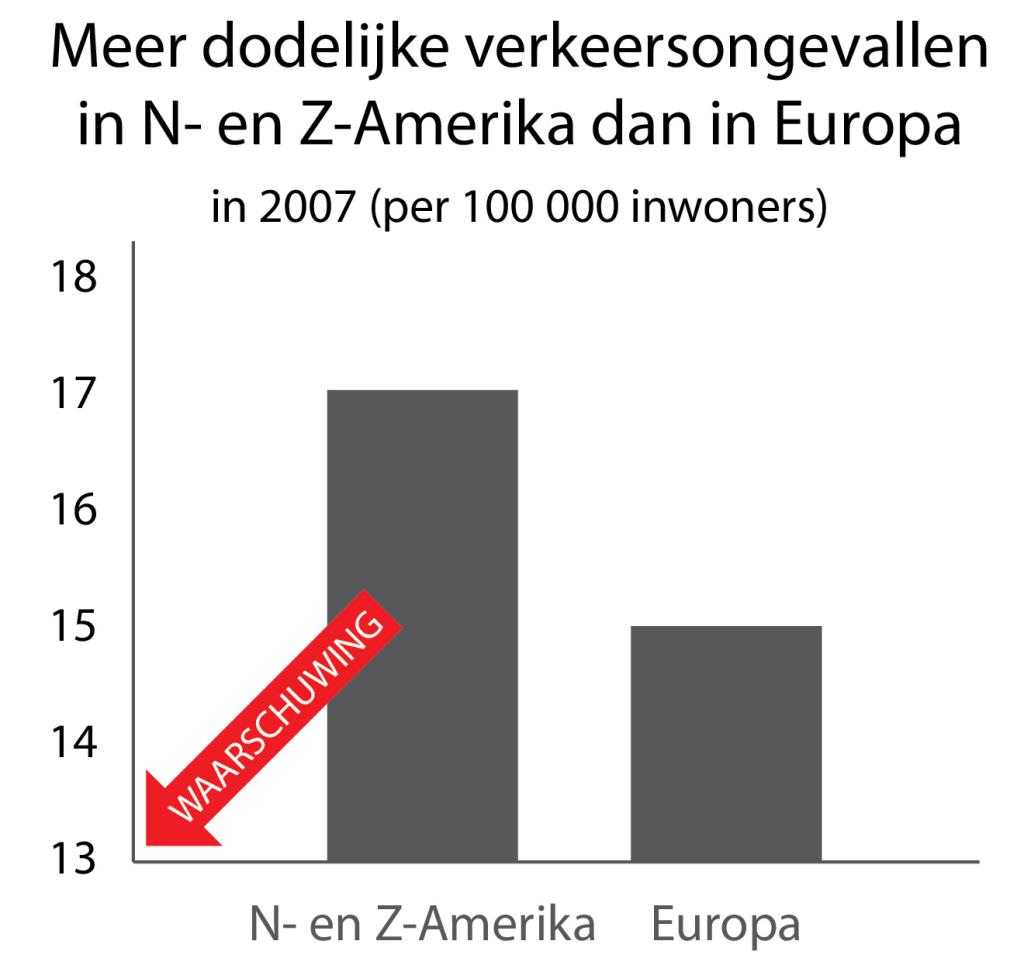
Correctiemethode C waarschuwt met een tekst voor de afgesneden y-as:
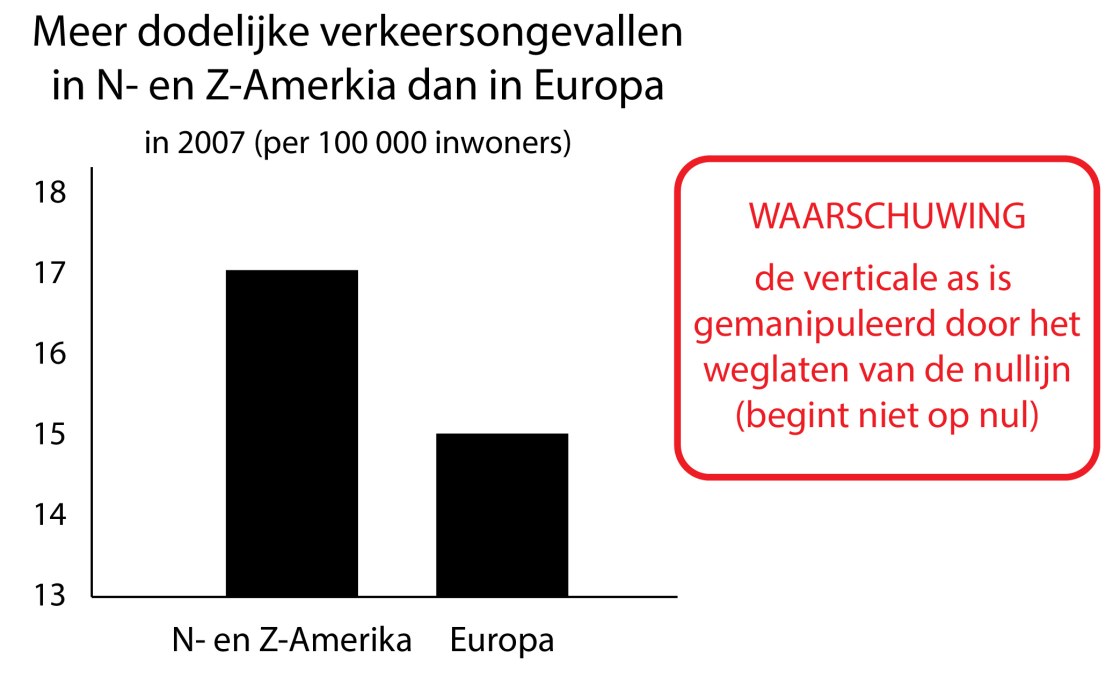
Correctiemethode D waarschuwt in algemene bewoordingen voor de misleidende weergave van data:
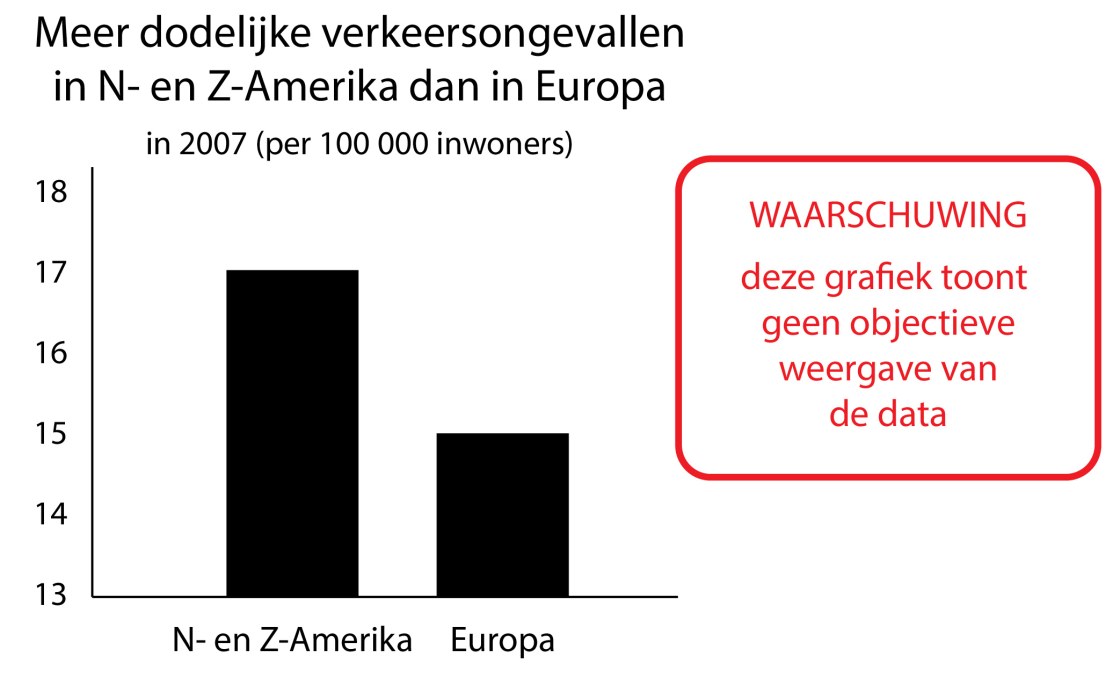
Presenteer een kloppende grafiek als alternatief
Alle vier de methodes bleken effectief, maar de eerste (A) werkte het best: de meest effectieve methode om misleidende grafieken te debunken, is door het beeld letterlijk te overschrijven met een accuraat alternatief. Deze correctiemethode grijpt in op de eerste fase van grafieken lezen waarin mensen een intuïtieve eerste inschatting maken van de data. De deelnemers die deze methode voorgeschoteld kregen, bleken het beste in staat om een betere inschatting te maken van de misleidende grafieken, dat wil zeggen: een inschatting die dicht lag bij hoe de accurate versie van de grafiek werd beoordeeld door de andere deelnemers.
Om te onderzoeken of het effect van de correctie beklijfde, vroegen we dezelfde deelnemers een week later opnieuw de grafieken uit de eerste serie te beoordelen, en ook evenveel nieuwe misleidende en accurate grafieken. Daarbij was nog steeds een klein effect zichtbaar dat voor alle vier de methodes vrijwel even groot was.
Opzet van het onderzoek
Voor dit onderzoek hebben 440 deelnemers (Amerikanen, representatief verdeeld naar leeftijd en geslacht) een vragenlijst ingevuld. Zij waren over het algemeen iets bovengemiddeld opgeleid en hadden een gemiddelde tot hoge grafiekgeletterdheid.
Zij kregen een serie te zien van misleidende grafieken met een afgesneden verticale as en accurate grafieken met een verticale as die op nul begint. Alle grafieken hadden twee staven en de deelnemers moesten steeds aangeven hoe groot zij het verschil tussen de staven vonden op een horizontale lijn die liep van “zeer klein” tot “zeer groot”. Van de misleidende grafieken die aan de ene helft van de deelnemers werden getoond, werden accurate versies aan de andere helft getoond, en andersom.
Vervolgens kregen alle deelnemers correcties te zien van de misleidende grafieken uit de eerste serie en moesten zij opnieuw het verschil tussen de staven beoordelen. Voor deze serie met correcties werden de deelnemers in vier groepen verdeeld (één groep per correctiemethode) en kreeg elke deelnemer steeds dezelfde correctiemethode voorgeschoteld. Daarna kregen de deelnemers nog een serie met nieuwe gerandomiseerde misleidende en accurate grafieken te zien om te beoordelen. Een week later volgde nog een vragenlijst met misleidende en accurate grafieken.
Misleiding meten
Om na te gaan of de misleidende grafieken ook echt misleidend werkten, hebben we gekeken hoe ver de gemiddelde beoordeling van elke misleidende grafiek af lag van de gemiddelde beoordeling van de accurate versie van die grafiek die door de andere helft van de groep werd beoordeeld. Alle misleidende grafieken bleken de deelnemers inderdaad te hebben misleid: het verschil tussen de staven in de misleidende grafieken werd significant als groter beoordeeld dan in de accurate grafieken. Deze uitkomst was er ongeacht opleiding of grafiekgeletterdheid, al was de misleiding bij niet-wetenschappelijk geschoolden en laag grafiekgeletterden over het algemeen groter.
Om de effectiviteit van de correctiemethoden te meten, werd gekeken hoe ver de deelnemers in hun beoordeling opschoven als ze na het zien van de misleidende grafiek de correctie voorgeschoteld kregen. Alle correctiemethoden bleken effectief voor het naar beneden bijstellen van de beoordeling (het verschil tussen de staven werd als minder groot ervaren in de gecorrigeerde grafiek), maar methode A stak er met kop en schouders bovenuit.
De effectiviteit van de correctiemethoden op de langere termijn is getest door de beoordeling van de misleidende grafieken uit de eerste serie te vergelijken met de beoordeling ervan een week later. De beoordeling van misleidende grafieken na een week lag voor alle methoden lager dan vóór de correctie, maar was niet meer zo laag als tijdens de correctie. Het effect bleef dus wel een week hangen, maar het werd minder sterk.
Vervolgonderzoek naar grafiekgeletterdheid
Misleiding ligt voor iedereen op de loer, ongeacht opleiding of ervaring met grafieken lezen, al zijn niet-wetenschappelijk geschoolden en lager geletterden wel kwetsbaarder. Als vervolg op het net gepubliceerde onderzoek komt er een nieuw experiment met jonge deelnemers (16-20 jaar) die een mbo-opleiding volgen.
De focus zal liggen op het optimaliseren van het ontwerp van de meest effectieve correctiemethode. In dit nieuwe onderzoek zal ook de variëteit worden verbreed naar meer typen grafieken en meer vormen van misleiding: naast staafdiagrammen met afgesneden verticale assen testen we onder meer 3D-taartdiagrammen. De opmaak wordt realistischer door meer kleur en designelementen op te nemen.
Nieuwe rubriek: Grafiekpolitie
Om de grafiekgeletterdheid bij onze lezers te bevorderen, begint Nieuwscheckers met de nieuwe rubriek Grafiekpolitie. In de eerste aflevering laten we zien wat er niet klopt in een infographic met bomen van Rijkswaterstaat. Tips zijn welkom – mail ons.



